Historicamente, a ideia de seu uso baseia-se na Garrafa de Leiden inventada acidentalmente em 1746 por Pieter van Musschenbroek na cidade de Leyden na Holanda.
Exemplos de capacitores
Física do capacitor
Visão geral
Os formatos típicos consistem em dois eletrodos ou placas que armazenam cargas opostas. Estas duas placas são condutoras e são separadas por um isolante ou por um dielétrico. A carga é armazenada na superfície das placas, no limite com o dielétrico. Devido ao fato de cada placa armazenar cargas iguais, porém opostas, a carga total no dispositivo é sempre zero.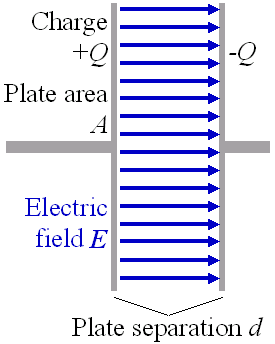
Quando uma diferença de potencial V = Ed é aplicada às placas deste capacitor simples, surge um campo elétrico entre elas. Este campo elétrico é produzido pela acumulação de uma carga nas placas.
Capacitância
A propriedade que estes dispositivos têm de armazenar energia elétrica sob a forma de um campo eletrostático é chamada de capacitância ou capacidade (C) e é medida pelo quociente da quantidade de carga (Q) armazenada pela diferença de potencial ou tensão (V) que existe entre as placas:A equação acima é exata somente para valores de Q muito maiores que a carga do elétron (e = 1,602 × 10−19 C). Por exemplo, se uma capacitância de 1 pF fosse carregada a uma tensão de 1 µV, a equação perderia uma carga Q = 10−19 C, mas isto seria impossível já que seria menor do que a carga em um único elétron. Entretanto, as experiências e as teorias recentes sugerem a existência de cargas fracionárias.
A capacitância de um capacitor de placas paralelas constituído de dois eletrodos planos idênticos de área A separados à distância constante d é aproximadamente igual a:
- C é a capacitância em faraday
- ε0 é a permissividade eletrostática do vácuo ou espaço livre
- εr é a constante dielétrica ou permissividade relativa do isolante utilizado.
Energia
A energia (no SI, medida em Joules) armazenada em um capacitor é igual ao trabalho feito para carregá-lo. Considere um capacitor com capacitância C, com uma carga +q em uma placa e -q na outra. Movendo um pequeno elemento de carga dq de uma placa para a outra contra a diferença de potencial V = q/C necessita de um trabalho dW:
Os elétrons das moléculas mudam em direção à placa da esquerda positivamente carregada. As moléculas então criam um campo elétrico do lado esquerdo que anula parcialmente o campo criado pelas placas. (O espaço do ar é mostrado para maior clareza; em um capacitor real, o dielétrico fica em contato direto com as placas.)
Circuitos elétricos
Os elétrons não podem passar diretamente através do dielétrico de uma placa do capacitor para a outra. Quando uma tensão é aplicada a um capacitor através de um circuito externo, a corrente flui para uma das placas, carregando-a, enquanto flui da outra placa, carregando-a, inversamente. Em outras palavras, quando a Tensão que flui por um capacitor muda, o capacitor será carregado ou descarregado. A fórmula corrente é dada porNo caso de uma tensão contínua (DC ou também designada CC) logo um equilíbrio é encontrado, onde a carga das placas correspondem à tensão aplicada pela relação Q=CV, e nenhuma corrente mais poderá fluir pelo circuito. Logo a corrente contínua (DC) não pode passar. Entretanto, correntes alternadas (AC) podem: cada mudança de tensão ocasiona carga ou descarga do capacitor, permitindo desta forma que a corrente flua. A quantidade de "resistência" de um capacitor, sob regime AC, é conhecida como reatância capacitiva, e a mesma varia conforme varia a frequência do sinal AC. A reatância capacitiva é dada por:
- XC = reatância capacitiva, medida em ohms
- f = frequência do sinal AC, em Hertz - Hz
- C = capacitância medida em Farads F
É denominada reatância pois o capacitor reage a mudanças na tensão, ou diferença de potencial.
Desta forma a reatância é proporcionalmente inversa à frequência do sinal. Como sinais DC (ou CC) possuem frequência igual a zero, a fórmula confirma que capacitores bloqueiam completamente a corrente aplicada diretamente, após um determinado tempo, em que o capacitor está carregando. Para correntes alternadas (AC) com frequências muito altas a reatância, por ser muito pequena, pode ser desprezada em análises aproximadas do circuito.
A impedância de um capacitor é dada por:
Portanto, a reatância capacitiva é o componente imaginário negativo da impedância.
Em um circuito sintonizado tal como um receptor de rádio, a frequência selecionada é uma função da indutância (L) e da capacitância (C) em série, como dado em
Associação de capacitores
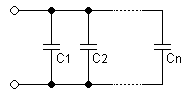
Num circuito de condensadores montados em paralelo todos estão sujeitos à mesma diferença de potencial (tensão). Para calcular a sua capacidade total (Ceq):Capacitores na prática
Capacitores comuns
Apresenta-se com tolerâncias de 5 % ou 10 %.Capacitores são frequentemente classificados de acordo com o material usado como dielétrico. Os seguintes tipos de dielétricos são usados:
- cerâmica (valores baixos até cerca de 1 μF)
- C0G ou NP0 - tipicamente de 4,7 pF a 0,047 uF, 5 %. Alta tolerância e performance de temperatura. Maiores e mais caros
- X7R - tipicamente de 3300 pF a 0,33 uF, 10 %. Bom para acoplamento não-crítico, aplicações com timer.
- Z5U - tipicamente de 0,01 uF a 2,2 uF, 20 %. Bom para aplicações em bypass ou acoplamentos. Baixo preço e tamanho pequeno.
- poliestireno (geralmente na escala de picofarads)
- poliéster (de aproximadamente 1 nF até 10 μF)
- polipropilêno (baixa perda. alta tensão, resistente a avarias)
- tântalo (compacto, dispositivo de baixa tensão, de até 100 μF aproximadamente)
- eletrolítico (de alta potência, compacto mas com muita perda, na escala de 1 μF a 1000 μF)
Já que capacitores têm ESRs tão baixos, eles têm a capacidade de entregar correntes enormes em circuitos curtos, o que pode ser perigoso. Por segurança, todos os capacitores grandes deveriam ser descarregados antes do manuseio. Isso é feito colocando-se um resistor pequeno de 1 ohm a 10 ohm nos terminais, isso é, criando um circuito entre os terminais, passando pelo resistor.
Capacitores também podem ser fabricados em aparelhos de circuitos integrados de semicondutores, usando linhas metálicas e isolantes num substrato. Tais capacitores são usados para armazenar sinais analógicos em filtros chaveados por capacitores, e para armazenar dados digitais em memória dinâmica de acesso aleatória (DRAM). Diferentemente de capacitores discretos, porém, na maior parte do processo de fabricação, tolerâncias precisas não são possíveis (15 % a 20 % é considerado bom).
Identificação do valor no capacitor cerâmico
Os capacitores cerâmicos apresentam impressos no próprio corpo um conjunto de três algarismos e uma letra. Para se obter o valor do capacitor os dois primeiros algarismos representam os dois primeiros dígitos do valor do capacitor, e o terceiro algarismo (algarismo multiplicador) representa o número de zeros à direita. A letra representa a tolerância do capacitor (a qual pode ser omitida), que é a faixa de valores em que a capacitância variará. Para os capacitores cerâmicos até 10pF esta é expressa em pF. Para os acima de 10pF é expressa em porcentagem. Por exemplo um capacitor com 224F impresso no próprio corpo, possuirá uma capacitância de 220000pF com uma tolerância de +/- 1% (seu valor pode ser um ponto percentual à mais ou à menos desse valor).Identificação do valor no capacitor de poliéster
Para a identificação dos valores do capacitor de poliéster é usado um conjunto de 7 faixas coloridas (conforme tabela), embora seja um método em desuso pelos fabricantes, no qual cada faixa representará respectivamente:primeiro algarismo,segundo algarismo, algarismo multiplicador, tolerância e tensão.O valor é obtido em pF.Capacitores variáveis
Há dois tipos distintos de capacitores variáveis, cujas capacitâncias podem ser mudadas intencionalmente e repetidamente ao longo da vida do dispositivo:- Aqueles que usam uma construção mecânica para mudar a distância entre as placas, ou a superfície da área das placas superpostas. Esses dispositivos são chamados capacitores de sintonia, ou simplesmente "capacitores variáveis", e são usados em equipamentos de telecomunicação para sintonia e controle de frequências.Neste tipo de capacitor o elemento dielétrico é o próprio ar.
- Aqueles que usam o fato de que a espessura da camada de depleção de um diodo varia com a tensão da corrente contínua atravessando o diodo. Esses diodos são chamados de diodos de capacitância variável, varactores ou varicaps. Qualquer diodo exibe esse efeito, mas dispositivos vendidos especificamente como varactores têm uma área de junção grande e um perfil de dopagem especificamente dimensionado para maximizar a capacitância.
- Em um capacitor microfone (comumente conhecido como um microfone condensador), o diafragma age como uma placa do capacitor, e as vibrações produzem alterações na distância entre o diafragma e uma placa fixa, alterando a tensão entre as placas.
Capacitores de Camada Dupla Elétrica (EDLCs)
Esses dispositivos, frequentemente chamados de supercapacitores ou ultracapacitores para simplificar, são capacitores que usam uma camada de eletrolítico de espessura molecular, ao invés de uma folha manufaturada de material, como o dielétrico. Como a energia armazenada é inversamente proporcional à espessura do dielétrico, esses capacitores têm uma densidade de energia extremamente alta. Os eletrodos são feitos de carbono ativado, que tem uma área de superfície alta por unidade de volume, aumentando a densidade de energia do capacitor. EDLCs individuais têm capacitâncias de centenas ou até milhares de farads.Os EDLCs podem ser usados como substitutos para baterias em aplicações em que uma grande corrente de descarga seja necessária. Eles também podem ser recarregados centenas de milhares de vezes, diferentemente das baterias convencionais que duram apenas algumas poucas centenas ou milhares de ciclos de recarga.
Aplicações
Capacitores são comumente usados em fontes de energia onde elas suavizam a saída de uma onda retificada completa ou meia onda.Por passarem sinais de Corrente Alternada mas bloquearem Corrente Contínua, capacitores são frequentemente usados para separar circuitos Corrente alternada de corrente continua. Este método é conhecido como acoplamento AC.
Capacitores também são usados na correção de fator de potência. Tais capacitores frequentemente vêm como três capacitores conectados como uma carga trifásica. Geralmente, os valores desses capacitores não são dados pela sua capacitância, mas pela sua potência reativa em var.
História
A Jarra de Leyden foi a primeira forma de capacitor. Fora inventada na Universidade de Leyden, na Holanda por Pieter van Musschenbroek. Ela era uma jarra de vidro coberta interna e externamente, mas sem se tocarem, com metal. A cobertura interna era conectada a uma vareta que saia pelo gargalo da jarra e terminava numa bola de metal, desta forma o vidro da jarra comportava-se como o dielétrico armazenador das cargas elétricas e os metais das paredes interna e externa como as armaduras deste capacitor primitivo.Corrente de Deslocamento
O físico James Clerk Maxwell inventou o conceito de corrente de deslocamento, dD/dt, para tornar a Lei de Ampère consistente com a conservação de carga em casos em que a carga se acumula, como por exemplo num capacitor. Ele interpretou este fenômeno como um movimento real de cargas, mesmo no vácuo, onde ele supôs que corresponderia ao movimento de cargas de um dipolo no éter. Embora essa interpretação tenha sido abandonada, a correção de Maxwell à lei de Ampere permanece válida (um campo elétrico variável produz um campo magnético).A corrente de deslocamento deve ser incluída, por exemplo, para aplicação das Leis de Kirchhoff a um capacitor.

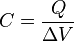
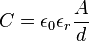




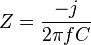
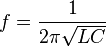






Nenhum comentário:
Postar um comentário